Category: volatility arbitrage

Profitability of Dispersion Trading in Liquid and Less Liquid Environments

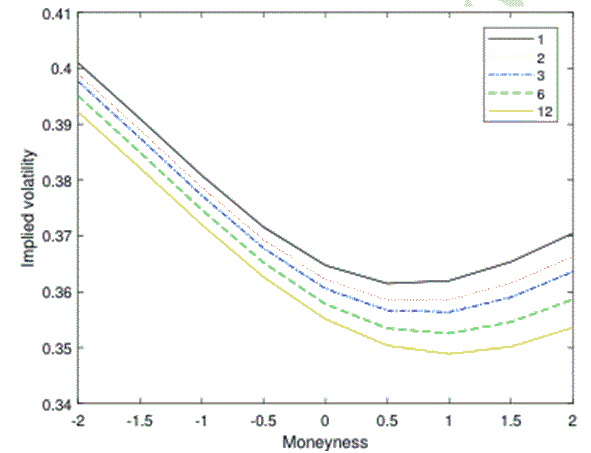
Dispersion trading is an investment strategy used to capitalize on discrepancies in volatilities between an index and its constituents. In this issue, I will feature dispersion trading strategies and discuss their profitability.

Profitability of a Dispersion Trading Strategy

Reference [1] provided an empirical analysis of a dispersion trading strategy to verify its profitability. The return of the dispersion trading strategy was 23.51% per year compared to the 9.71% return of the S&P 100 index during the same period. The Sharpe ratio of the dispersion trading strategy was 2.47, and the portfolio PnL had a low correlation (0.0372) with the S&P 100 index.

Findings

-The article reviews the theoretical foundation of dispersion trading and frames it as an arbitrage strategy based on the mispricing of index options due to overestimated implied correlations among the index’s constituents.

-The overpricing phenomenon is attributed to the correlation risk premium hypothesis and the market inefficiency hypothesis.

-Empirical evidence shows that a basic dispersion trading strategy—using at-the-money straddles on the S&P 100 and a representative subset of its stocks—has significantly outperformed the broader stock market.

-The performance of the dispersion strategy demonstrated a very low correlation to the S&P 100 index, highlighting its diversification potential.

-This study reinforces the idea that sophisticated options strategies can uncover persistent market inefficiencies.

This article proved the viability of the dispersion trading strategy. However, there exist two issues related to execution,

-The analysis assumes no transaction costs, which is a key limitation; in practice, only market makers might replicate the back-tested performance due to the absence of slippage.

-Another limitation is the simplified delta hedging method used, which was based on daily rebalancing.

-A more optimized hedging approach could potentially yield higher returns and partially offset transaction costs.

Reference

[1] P. Ferrari, G. Poy, and G. Abate, Dispersion trading: an empirical analysis on the S&P 100 options, Investment Management and Financial Innovations, Volume 16, Issue 1, 2019

Dispersion Trading in a Less Liquid Market

The previous paper highlights some limitations of the dispersion strategy. Reference [2] further explores issues regarding liquidity. It investigates the profitability of dispersion trading in the Swedish market.

Findings

-Dispersion trading offers a precise and potentially profitable approach to hedging vega risk, which relates to volatility exposure.

-The strategy tested involves shorting OMXS30 index volatility and taking a long volatility position in a tracking portfolio to maintain a net vega of zero.

-The backtesting results show that vega risk can be accurately hedged using dispersion trading.

– Without transaction costs, the strategy yields positive results.

-However, after accounting for the bid-ask spread, the strategy did not prove to be profitable over the simulated period.

– High returns are offset by substantial transaction costs due to daily recalibration of tracking portfolio weights.

– Less frequent rebalancing reduces transaction costs but may result in a worse hedge and lower correlation to the index.

In short, the study concluded that if we use the mid-price, then dispersion trading is profitable. However, when considering transaction costs and the B/A spreads, the strategy becomes less profitable.

I agree with the author that the strategy can be improved by hedging less frequently. However, this will lead to an increase in PnL variance. But we note that this does not necessarily result in a smaller expected return.

Reference

[2] Albin Irell Fridlund and Johanna Heberlei, Dispersion Trading: A Way to Hedge Vega Risk in Index Options, 2023, KTH Royal Institute of Technology

Closing Thoughts

I have discussed the profitability of dispersion strategies in both liquid and illiquid markets. There exist “inefficiencies” that can be exploited, but doing so requires a more developed hedging approach and solid infrastructure. The “edge” is apparent, but consistently extracting it demands a high level of skill, discipline, and operational capability. In reality, it is this latter part, i.e. the ability to build and maintain the necessary infrastructure, that represents the true edge.

Breaking Down Volatility: Diffusive vs. Jump Components

Implied volatility is an important concept in finance and trading. In this post, I further discuss its breakdown into diffusive volatility and jump risk components.

Decomposing Implied Volatility: Diffusive and Jump Risks

Implied volatility is an estimation of the future volatility of a security’s price. It is calculated using an option-pricing model, such as the Black-Scholes-Merton model.

Reference [1] proposed a method for decomposing implied volatility into two components: a volatility component and a jump component. The volatility component is the price of a portfolio only bearing volatility risks and the jump component is the price of a portfolio only bearing jump risks. The decomposition is made by constructing two option portfolios: a delta- and gamma-neutral but vega-positive portfolio and a delta- and vega-neutral but gamma-positive portfolio. These portfolios bear volatility and jump risks respectively.

Findings

– The study examines the return patterns of straddles and their component portfolios, focusing on jump risk and volatility risk around earnings announcements.

– The findings show that straddle returns closely resemble those of the jump risk portfolio, suggesting that the options market prioritizes earnings jump risk during these events.

– The research highlights the significant role of earnings jump risk in financial markets, as it is substantially priced into straddles and influences both options and stock market behavior.

– A proposed straddle price decomposition method and the S-jump measure could be applied to other market events, such as M & A and natural disasters, to assess risk and pricing dynamics.

This paper discussed an important concept in option pricing theory; that is, the implied volatilities, especially those of short-dated options, comprise not only volatility but also jump risks.

Reference

[1] Chen, Bei and Gan, Quan and Vasquez, Aurelio, Anticipating Jumps: Decomposition of Straddle Price (2022). Journal of Banking and Finance, Volume 149, April 2023, 106755

Measuring Jump Risks in Short-Dated Option Volatility

Unlike long-dated options, short-dated options incorporate not only diffusive volatility but also jump risks. One of the earliest works examining the jump risks is by Carr et al [2].

Reference [3] developed a stochastic jump volatility model that includes jumps in the underlying asset. It then constructed a skew index, a so-called crash index.

Findings

-This paper introduces a novel methodology to measure forward-looking crash risk implied by option prices, using a tractable stochastic volatility jump (SVJ) model.

-The approach isolates the jump size component from the stochastic volatility embedded within uncertainty risk, extending beyond the Black-Scholes-Merton framework.

-The methodology parallels the construction of implied volatility surfaces, enabling the development of an option-implied crash-risk curve (CIX).

-The CIX is strongly correlated with non-parametric option-implied skewness but offers a more refined measure of crash risk by adjusting for stochastic volatility (Vt) and emphasizing tail risk dynamics.

-In contrast, option-implied skewness reflects both crash and stochastic volatility risks, presenting smoother characteristics of the risk-neutral density.

-Empirical analysis reveals a notable upward trend in the CIX after the 2008 financial crisis, aligning with narratives on rare-event risks and emphasizing the value of incorporating such beliefs into asset pricing frameworks.

References

[2] P Carr, L Wu, What type of process underlies options? A simple robust test, The Journal of Finance, 2003

[3] Gao, Junxiong and Pan, Jun, Option-Implied Crash Index, 2024. SSRN

Closing Thoughts

In this issue, I discussed the breakdown of volatility into diffusive and jump components. Understanding this distinction is important for trading, and risk management in theory and practice.

Capturing Volatility Risk Premium Using Butterfly Option Strategies

The volatility risk premium is a well-researched topic in the literature. However, less attention has been given to specific techniques for capturing it. In this post, I’ll highlight strategies for harvesting the volatility risk premium.

Long-Term Strategies for Harvesting Volatility Risk Premium

Reference [1] discusses long-term trading strategies for harvesting the volatility risk premium in financial markets. The authors emphasize the unique characteristics of the volatility risk premium factor and propose trading strategies to exploit it, specifically for long-term investors.

Findings

– Volatility risk premium is a well-known phenomenon in financial markets.

– Strategies designed for volatility risk premium harvesting exhibit similar risk/return characteristics. They lead to a steady rise in equity but may suffer occasional significant losses. They’re not suitable for long-term investors or investment funds with less frequent trading.

– The paper examines various volatility risk premium strategies, including straddles, butterfly spreads, strangles, condors, delta-hedged calls, delta-hedged puts, and variance swaps.

– Empirical study focuses on the S&P 500 index options market. Variance strategies show substantial differences in risk and return compared to other factor strategies.

– They are positively correlated with the market and consistently earn premiums over the study period. They are vulnerable to extreme stock market crashes but have the potential for quick recovery.

– The authors conclude that volatility risk premium is distinct from other factors, making it worthwhile to implement trading strategies to harvest it.

Reference

[1] Dörries, Julian and Korn, Olaf and Power, Gabriel, How Should the Long-term Investor Harvest Variance Risk Premiums? The Journal of Portfolio Management   50 (6) 122 – 142, 2024

Trading Butterfly Option Positions: a Long/Short Approach

A butterfly option position is an option structure that requires a combination of calls and/or puts with three different strike prices of the same maturity. Reference [2] proposes a novel trading scheme based on butterflies’ premium.

Findings

– The study calculates the rolling correlation between the Cboe Volatility Index (VIX) and butterfly options prices across different strikes for each S&P 500 stock.

– The butterfly option exhibiting the strongest positive correlation with the VIX is identified as the butterfly implied return (BIR), indicating the stock’s expected return during a future market crash.

– Implementing a long-short strategy based on BIR allows for hedging against market downturns while generating an annualized alpha ranging from 3.4% to 4.7%.

-Analysis using the demand system approach shows that hedge funds favor stocks with a high BIR, while households typically take the opposite position.

-The strategy experiences negative returns at the bottom of a market crash, making it highly correlated with the pricing kernel of a representative household.

-The value-weighted average BIR across all stocks represents the butterfly implied return of the market (BIRM), which gauges the severity of a future market crash.

-BIRM has a strong impact on both the theory-based equity risk premium (negatively) and the survey-based expected return (positively).

This paper offers an interesting perspective on volatility trading. Usually, in a relative-value volatility arbitrage strategy, implied volatilities are used to assess the rich/cheapness of options positions. Here the authors utilized directly the option positions premium to evaluate their relative values.

Reference

[2] Wu, Di and Yang, Lihai, Butterfly Implied Returns, SSRN 3880815

Closing Thoughts

In summary, both papers explore strategies for capturing the volatility risk premium. The first paper highlights the distinct characteristics of the volatility risk premium and outlines trading strategies tailored for long-term investors. The second paper introduces an innovative trading scheme centered around butterfly option structures. Together, these studies contribute valuable insights into optimizing risk-adjusted returns through strategic volatility trading.

Volatility Risk Premium: The Growing Importance of Overnight and Intraday Dynamics

The breakdown of the volatility risk premium into overnight and intraday sessions is an active and emerging area of research. It holds not only academic interest but also practical implications. ETF issuers are launching new ETFs to capitalize on the overnight risk premium, and the shift toward around-the-clock trading could impact the VRP and popular strategies such as covered call writing. In this post, I’ll discuss the VRP breakdown, its implications, impact, and more.

Volatility Risk Premium is a Reward for Bearing Overnight Risk

The volatility risk premium (VRP) represents the difference between the implied volatility of options and the realized volatility of the underlying asset. Reference [1] examines the asymmetry in the VRP. Specifically, it investigates the VRP during the day and overnight sessions. The research was conducted in the Nifty options market, but previous studies in the S&P 500 market reached the same conclusion.

Findings

– There is a significant difference in returns between overnight and intraday short option positions, unrelated to a weekend effect.

– The return asymmetry decreases as option moneyness and maturity increase.

– A systematic relationship exists between day-night option returns and the option Greeks.

– Average post-noon returns are significantly negative for short call positions and positive for short put positions, while pre-noon returns are largely insignificant, indicating that the VRP varies throughout the trading day for calls and puts.

– A significant jump in the underlying index reduces the day-night disparity in option returns due to increased implied volatilities, which boost both intraday and overnight returns.

– Strong positive overnight returns suggest that the VRP in Nifty options prices mainly compensates for overnight risk.

– A strategy of selling index options at the end of the trading day and covering them at the beginning of the next day yields positive returns before transaction costs but is not profitable after accounting for transaction costs.

Reference

[1] Aparna Bhat, Piyush Pandey, S. V. D. Nageswara Rao, The asymmetry in day and night option returns: Evidence from an emerging market, J Futures Markets, 2024, 1–18

Inventory Risk and Its Impact on the Volatility Risk Premium

The previous paper suggests that the VRP is specifically a reward for bearing overnight risk. Reference [2] goes further by attempting to answer why this is the case. It provides an explanation in terms of market makers’ inventory risks, as they hold a net-short position in put options.

Findings

-Put option risk premia are significantly negative overnight when equity exchanges are closed and continuous delta-hedging is not feasible.

-Intraday, when markets are liquid and delta-hedging is possible, put option risk premia align with the risk-free rate.

-Call options show no significant risk premia during the sample period.

-Market makers’ short positions in puts expose them to overnight equity price “gap” risks, while their call option positions are more balanced between long and short, resulting in minimal exposure to gap risk.

-Increased overnight liquidity reduces option risk premia. Regulatory changes and the acquisition of major electronic communication networks in 2006 boosted overnight equity trade volumes from Monday to Friday, reducing the magnitude of weekday option risk premia compared to weekend risk premia.

-The study concludes that the S&P 500 option risk premium arises from a combination of options demand and overnight equity illiquidity.

An interesting implication of this research is that the introduction of around-the-clock trading could potentially reduce the VRP.

Reference

[2] J Terstegge, Intermediary Option Pricing, 2024, Copenhagen Business School

Closing Thoughts

Understanding the breakdown of the volatility risk premium into overnight and intraday components is crucial for both researchers and practitioners. As ETF issuers develop products to leverage the overnight risk premium and markets move toward 24-hour trading, these dynamics could significantly impact volatility strategies. Recognizing these shifts can help investors refine their approaches and adapt to evolving market conditions.

Hedging Efficiently: How Optimization Improves Tail Risk Protection

Tail risk hedging aims to protect portfolios from extreme market downturns by using strategies such as out-of-the-money options or volatility products. While effective in mitigating large losses, the challenge lies in balancing cost and long-term returns. In this post, we’ll discuss tail risk hedging and whether it can be done at a reasonable cost.

Tail Risk Hedging Strategies: Are They Effective?

Tail risk hedging involves purchasing put options to protect the portfolio either partially or fully. Reference [1] presents a study of different tail risk hedging strategies. It explores the effectiveness of put option monetization strategies in protecting equity portfolios and enhancing returns.

Findings

– Eight different monetization strategies were applied using S&P 500 put options and the S&P 500 Total Return index from 1996 to 2020.

– Results compared against an unhedged index position and a constant volatility strategy on the same underlying index.

– Tail risk hedging, in this study, yielded inferior results in terms of risk-adjusted and total returns compared to an unhedged index position.

– Over a 25-year period, all strategies’ total returns and Sharpe ratios were worse than the unhedged position.

– Buying puts involves paying for the volatility risk premium, contributing to less favorable results.

– The results are sensitive to choices of time to expiry and moneyness of purchased options in tested strategies.

– The authors suggest the possibility of minimizing hedging costs by optimizing for strikes and maturities.

Reference:

[1] C.V. Bendiksby, MOJ. Eriksson, Tail-Risk Hedging An Empirical Study, Copenhagen Business School

How Can Put Options Be Used in Tail Risk Hedging?

The effectiveness of using put options to hedge the tail risks depends on the cost of acquiring put options, which can eat into investment returns. Reference [2] proposes a mixed risk-return optimization framework for selecting long put options to hedge S&P 500 tail risk. It constructs hypothetical portfolios that continuously roll put options for a tractable formulation.

Findings

– The article discusses the effectiveness of tail risk hedging. It highlights that the premium paid for put options can be substantial, especially when continuously renewing them to maintain protection. This cost can significantly impact investment returns and overall portfolio performance.

– The article introduces an optimization-based approach to tail-risk hedging, using dynamic programming with variance and CVaR as risk measures. This approach involves constructing portfolios that constantly roll over put options, providing protection without losing significant long-term returns.

– Contrary to previous research, the article suggests that an effective tail-risk hedging strategy can be designed using this optimization-based approach, potentially overcoming the drawbacks of traditional protective put strategies.

-The proposed hedging strategy overcame traditional drawbacks of protective put strategies. It outperforms both direct investments in the S&P 500 and static long put option positions.

Reference

[2] Yuehuan He and Roy Kwon, Optimization-based tail risk hedging of the S&P 500 index, THE ENGINEERING ECONOMIST, 2023

Closing Thoughts

Tail risk hedging is expensive. While the first paper demonstrated that tail risk hedging leads to inferior returns, it suggested that results could be improved by optimizing strike prices and maturities. The second paper built on this idea and proposed a hedging scheme based on optimization. The proposed strategy outperforms both direct investments in the S&P 500 and static long put option positions.

PCA in Action: From Commodity Derivatives to Dispersion Trading

Principal Component Analysis (PCA) is a dimensionality reduction technique used to simplify complex datasets. It transforms the original variables into a smaller set of uncorrelated variables called principal components, ranked in order of their contribution to the dataset’s total variance. In this post, we’ll discuss various applications of PCA.

Pricing Commodity Derivatives Using Principal Component Analysis

Due to the seasonal nature of commodities, pricing models should be able to take into account seasonality and other deterministic factors.

Reference [1] proposed a new, multi-factor pricing method based on Principal Component Analysis (PCA). It introduces a multi-factor model designed to price commodity derivatives, with a particular focus on commodity swaptions.

Findings

– The model calibration process consists of two key steps: offline and online.

– The offline step, conducted infrequently, determines mean reversion rates, the ratio of long and short factor volatilities, and the correlation between the factors using historical data.

– The online step occurs every time the model is used to price an option or simulate price paths.

– Empirical analysis demonstrates that the model is highly accurate in its predictions and applications.

– Swaptions, which are relatively illiquid commodities, present a challenge due to their one-sided natural flow in the market.

– Model calibration strategies are divided into seasonal and non-seasonal categories, considering the asset’s characteristics. For seasonal assets like power or gas, local volatilities are calibrated separately for each contract, while a boot-strapping strategy is employed for non-seasonal assets like oil.

– Currently, the multi-factor model lacks a term structure for volatility ratios and mean reversions. However, it can be easily extended to incorporate a time dependency, which would facilitate fitting market prices of swaptions across various tenors.

Reference

[1]  Tim Xiao, Pricing Commodity Derivatives Based on A Factor Model, Philarchive

Dispersion Trading Using Principal Component Analysis

Dispersion trading involves taking positions on the difference in volatility between an index and its constituent stocks.

Reference [2] examined dispersion trading strategies based on a statistical index subsetting procedure and applied it to the S&P 500 constituents

Findings

– This paper introduces a dispersion trading strategy using a statistical index subsetting approach applied to S&P 500 constituents from January 2000 to December 2017.

– The selection process employs principal component analysis (PCA) to determine each stock’s explanatory power within the index and assigns appropriate subset weights.

– In the out-of-sample trading phase, both hedged and unhedged strategies are implemented using the most suitable stocks.

– The strategy delivers significant annualized returns of 14.52% (hedged) and 26.51% (unhedged) after transaction costs, with Sharpe ratios of 0.40 and 0.34, respectively.

– Performance remains robust across different market conditions and outperforms naive subsetting schemes and a buy-and-hold approach in terms of risk-return characteristics.

– A deeper analysis highlights a correlation between the chosen number of principal components and the behavior of the S&P 500 index.

– An index subsetting procedure was developed, considering the explanatory power of individual stocks, allowing a replicating option basket with as few as five securities.

– An analysis of sector exposure, principal components, and robustness checks demonstrated that the trading systems have superior risk-return characteristics compared to other dispersion strategies.

Reference

[2] L. Schneider, and J. Stübinger, Dispersion Trading Based on the Explanatory Power of S&P 500 Stock Returns, Mathematics 2020, 8, 1627

Closing Thoughts

PCA is a powerful tool in quantitative finance. In this issue, we have demonstrated its effectiveness in pricing commodity derivatives and developing dispersion trading strategies. Its versatility extends beyond these applications, making it a valuable technique for tackling a wide range of problems in quantitative finance.

Option Pricing Models and Strategies for Crude Oil Markets

Financial models and strategies are usually universal and can be applied across different asset classes. However, in some cases, they must be adapted to the unique characteristics of the underlying asset. In this post, I’m going to discuss option pricing models and trading strategies in commodities, specifically in the crude oil market.

Volatility Smile in the Commodity Market

Paper [1] investigates the volatility smile in the crude oil market and demonstrates how it differs from the smile observed in the equity market.  It proposes to use the new method developed by Carr and Wu in order to study the volatility smile of commodities. Specifically, the authors examine the volatility smile of the United States Oil ETF, USO.

Findings

– This paper examines the information derived from the no-arbitrage Carr and Wu formula within a new option pricing framework in the USO (United States Oil Fund) options market.

– The study investigates the predictability of this information in forecasting future USO returns.

– Using the no-arbitrage formula, risk-neutral variance, and covariance estimates are obtained under the new framework.

– The research identifies the term structure and dynamics of these risk-neutral estimates.

– The findings reveal a “U”-shaped implied volatility smile with a positive curvature in the USO options market.

Usually, an equity index such S&P 500 exhibits a downward-sloping implied volatility pattern, i.e. a negative implied volatility skew. Oil, on the other hand, possesses a different volatility smile. This is because while equities are typically associated with crash risks, oil prices exhibit both sharp spikes and crashes, leading to a different implied volatility pattern. This highlights the importance of considering the specific characteristics and dynamics of different asset classes when analyzing and interpreting implied volatility patterns.

Reference

[1] Xiaolan Jia, Xinfeng Ruan, Jin E. Zhang, Carr and Wu’s (2020) framework in the oil ETF option market, Journal of Commodity Markets, Volume 31, September 2023, 100334

Statistical Arbitrage in the Crude Oil Markets

Reference [2] directly applies statistical arbitrage techniques, commonly used in equity markets, to the crude oil market.  It utilizes cointegration to construct a statistical arbitrage portfolio. Various methods are then used to test for stationarity and mean reversion: the Quandt likelihood ratio (QLR), augmented Dickey-Fuller (ADF) test, autocorrelations, and the variance ratio. The constructed strategy performed well both in- and out-of-sample.

Findings

– This paper introduces the concept of statistical arbitrage through a trading strategy known as the mispricing portfolio.

– It focuses specifically on mean-reverting strategies designed to exploit persistent anomalies observed in financial markets.

– Empirical evidence is presented to demonstrate the effectiveness of statistical arbitrage in the crude oil markets.

– The mispricing portfolio is constructed using cointegration regression, establishing long-term pricing relationships between WTI crude oil futures and a replication portfolio composed of Brent and Dubai crude oils.

-Mispricing dynamics revert to equilibrium with predictable behaviour. Trading rules, which are commonly used in equity markets, are then applied to the crude oil market to exploit this pattern.

Reference

[2] Viviana Fanelli, Mean-Reverting Statistical Arbitrage Strategies in Crude Oil Markets, Risks 2024, 12, 106.

Closing Thoughts

As we’ve seen, techniques and models utilized in the equity market can sometimes be applied directly to the crude oil market, while other times they need to be adapted to the unique characteristics of the crude oil market. In any case, strong domain knowledge is essential.

Educational Video

In this webinar, Quantitative Trading in the Oil Market, Dr Ilia Bouchouev delivers an interesting and insightful presentation on algorithmic trading in the oil market. He also encourages viewers to apply the techniques discussed for the oil market to other markets, such as equities.

When Correlations Break or Hold: Strategies for Effective Hedging and Trading

It’s well known that there is a negative relationship between an equity’s price and its volatility. This can be explained by leverage or, alternatively, by volatility feedback effects. In this post, I’ll discuss practical applications to exploit this negative correlation between equity prices and their volatility.

A Trading Strategy Based on the Correlation Between the VIX and S&P500 Indices

This paper [1] examines the strong correlation in the S&P 500 and identifies trading opportunities when this correlation weakens or breaks down.

Findings

-The study covers the period from January 1995 to October 2020, utilizing 6,488 daily observations of the VIX and S&P500 indexes.

– In scenarios where the options market indicates increased drawdown risk with higher implied volatility but negative returns have not yet occurred, consider shorting the market.

– The signal to short the market occurs when the negative correlation between the S&P 500 and VIX is broken, and they start exhibiting a positive correlation.

– The test setup involves identifying one or two consecutive days with positive co-movement between the VIX and S&P 500, then setting the transaction date for the day after or at the close of the chosen date.

– Empirical results show that the strategy outperforms the S&P500 index over the 25-year period, achieving higher returns, lower systematic risk, and reduced volatility.

-The findings provide evidence that excess returns can be generated by timing the market using historical data, even after accounting for trading costs.

Reference

[1] Tuomas Lehtinen, Statistical arbitrage strategy based on VIX-to-market based signal, Hanken School of Economics

Optimal Hedging for Options Using Minimum-Variance Delta

Contrary to the first paper, Reference [2] focuses on the strong correlation between the S&P 500 and its volatility, designing an efficient scheme for hedging an options book.

The authors developed a so-called minimum variance (MV) delta. Essentially, the MV delta is the Black-Scholes delta with an additional adjustment term.

Findings

-Due to the negative relationship between price and volatility for equities, the minimum variance delta is consistently less than the practitioner Black-Scholes delta.

-Traders should under-hedge equity call options and over-hedge equity put options compared to the practitioner Black-Scholes delta.

-The study demonstrates that the minimum variance delta can be accurately estimated using the practitioner Black-Scholes delta and the historical relationship between implied volatilities and asset prices.

-The expected movement in implied volatility for stock index options can be approximated as a quadratic function of the practitioner Black-Scholes delta divided by the square root of time.

-A formula for converting the practitioner Black-Scholes delta to the minimum variance delta is provided, yielding good out-of-sample results for both European and American call options on stock indices.

-For S&P 500 options, the model outperforms stochastic volatility models and models based on the slope of the volatility smile.

-The model works less well for certain ETFs

Reference:

[2] John Hull and Alan White, Optimal Delta Hedging for Options, Journal of Banking and Finance, Vol. 82, Sept 2017: 180-190

Closing Thoughts

These two papers take opposing approaches: one exploits correlation breakdown, while the other capitalizes on the correlation remaining strong. However, they are not mutually exclusive. Combining insights from both can lead to a more efficient trading or hedging strategy.

Educational Video

This seminar by Prof. J. Hull delves into the second paper discussed above.

Abstract

The “practitioner Black-Scholes delta” for hedging equity options is a delta calculated from the Black-Scholes-Merton model with the volatility parameter set equal to the implied volatility. As has been pointed out by a number of researchers, this delta does not minimize the variance of a trader’s position. This is because there is a negative correlation between equity price movements and implied volatility movements. The minimum variance delta takes account of both the impact of price changes and the impact of the expected change in implied volatility conditional on a price change. In this paper, we use ten years of data on options on stock indices and individual stocks to investigate the relationship between the Black-Scholes delta and the minimum variance delta. Our approach is different from earlier research in that it is empirically-based. It does not require a stochastic volatility model to be specified. Joint work with Allan White.

Examining Contango and Backwardation in VIX Futures

In this post, I will continue exploring various aspects of the volatility index and the associated volatility futures.

Data

To conduct this study, data is essential. Below are the data sources:

  • Spot VIX: Yahoo Finance provides data but no longer allows direct downloads. With some programming, a workaround can be found, but the most convenient option is to use Barchart.

https://www.barchart.com/stocks/quotes/$VIX/price-history/historical

  • VX Futures: CBOE offers historical data in CSV format.

https://www.cboe.com/us/futures/market_statistics/historical_data/

  • Short-Term Futures Index:

While not directly utilized in this issue, I use this data to validate other ideas. For completeness, here is the download link:

https://www.spglobal.com/spdji/en/indices/indicators/sp-500-vix-short-term-index-mcap/#overview

Statistics for spot VIX and VX Futures

The table below provides statistics for the S&P 500 (tracked by SPY), spot VIX, and VX futures. It shows the percentage of days the S&P 500 index is up and the percentage of days VX futures are in contango, where the front-month futures price is lower than the next-month futures price.

From January 2013 to November 2024, the S&P 500 index was up  54.9% of the time, while VX futures were in contango most of the time (85.2%).

The next table presents the number of days VX futures were in backwardation while the spot VIX was in contango. Spot VIX in contango is defined as the 1M spot VIX being less than the 3M spot VIX.

From  January 2013 to July 2024, this situation was very rare, occurring only 7% of the time.  However, from  August 1 to November 4, 2024, this divergence occurred with much higher frequency, 53% of the time.

This situation presented a high reward/risk trade opportunity. For instance, one could structure a trade to capitalize on the high likelihood of VX futures returning to contango and a decline in the overall volatility level. One potential trade is buying a put option in VXX. We’ll discuss this strategy in an upcoming webinar.

Seasonality of Volatility

With the holiday season approaching, the equity world often discusses the “Santa Rally.” This raises the question: Is there any seasonality in the volatility market?

The graph below shows the average and median monthly implied and historical volatilities. A clear seasonal pattern is observed, with low volatility between April and July and high volatility in October. However, for December, there is no discernable pattern—volatility can be either high or low during this period.

Educational Video

This webinar by Prof Andrew Papanicolaou covers fundamental concepts of VX futures, such as contango, backwardation, and roll yield. It also presents an approach to modeling the VX futures term structure.

Abstract:

We study VSTOXX, VSTOXX futures and VSTOXX exchange-traded notes (ETNs) econometrically. We find that different rates of mean reversion capture fluctuations in the short and long maturities, respectively. We fit an exponential Ornstein-Uhlenbeck (OU) model to the data and find it to capable of simulating ETN time series that have similar properties to the historical observed ETN time series. We compare these results to a similar study performed on ETNs and futures for VIX. We also look at the joint behavior of VIX and VSTOXX futures, and explore portfolio allocation strategies among ETNs for both markets.

Closing Thoughts

The volatility market offers unique insights and opportunities for investors. By understanding concepts like contango, backwardation, and seasonality, we can structure strategies with favorable risk-reward profiles.

Let me know your thoughts in the comments below.

Making Use of Information Embedded in VIX Futures Term Structures

With the U.S. election now over, the VIX futures term structure has normalized. It typically follows the spot VIX term structure. However, before the election, the futures term structure was in backwardation while the spot VIX was in contango most of the time. This is a rare occurrence.  Below is a snapshot of the spot and futures term structures on September 26.

VIX futures term structure

In a future issue, I’ll present statistics and trade opportunities for such situations. In today’s issue, however, I will discuss two papers that develop trading systems for VIX futures.

Trading VIX Futures Using Neural Networks

Reference [1]  explores the use of neural networks, a type of artificial intelligence, to trade VIX futures. The authors assume that the term structure of VIX futures follows a Markov model. An interesting aspect of this paper is that it made use of a utility function to generate trading signals. The authors also performed thorough out-of-sample testing using the k-fold cross-validation technique.

The Model

  • The trading strategy aims to maximize expected utility for a day-ahead horizon considering the current shape and level of the term structure.
  • Computationally, a deep neural network with five hidden layers models the functional dependence between the VIX futures curve, positions, and expected utility.
  • Out-of-sample backtests indicate that this method achieves good portfolio performance.

Validation

  • The standard procedure for training involves dividing the data into two blocks: one for in-sample training and the other for out-of-sample testing.
  • VIX futures curves from April 14th, 2008, to August 7th, 2019, are used for in-sample training, while the remaining curves from August 8th, 2019, to November 5th, 2020, are used for out-of-sample testing.
  • Since the out-of-sample test is based on a single portfolio run, good performance could be attributed to luck. Therefore the method of k-fold cross-validation is applied.

Reference

[1] M. Avellaneda, T. N. Li, A. Papanicolaou, G. Wang, Trading Signals In VIX Futures, Applied Mathematical Finance. 2021;28(3):275–298

Trading VIX Futures Using Machine Learning Techniques

Building on the first paper, Reference [2] investigates machine learning techniques for trading VIX futures. It proposed using Constant Maturity Futures (CMF) to generate trading signals for VIX futures. It applied machine learning models to create these signals.

Findings

  • The experiment results show that term structure features, such as μt and ∆roll, are highly effective in predicting the next-day returns of VIX CMFs and offer potential economic benefits.
  • The C-MVO strategy outperformed the benchmark rank-based long-short strategy in backtesting across most machine learning models, offering valuable insights for trading VIX CMFs.
  • Neural network models, particularly ALSTM, demonstrated the best performance in both prediction and backtesting.
  • Tree-based models showed no clear superiority, while the linear regression model, which only considers linear relationships, outperformed all other models.
  • The findings highlight the predictive power of term structure features for next-day returns in VIX CMFs.

Reference

[2]  Wang S, Li K, Liu Y, Chen Y, Tang X (2024), VIX constant maturity futures trading strategy: A walk-forward machine learning study, PLoS ONE 19(4): e0302289

Closing Thoughts

These papers present trading systems developed using advanced techniques in machine learning and AI. As such, validation is critical. Techniques such as k-fold validation and walk-forward analysis should be carried out rigorously.

The research also suggests that there is valuable information embedded in the VIX futures term structure. In my opinion, “simple”, intuitive systems can be developed using VIX term structure that can provide decent risk-adjusted returns. Additionally, as I’ve discussed in one of my LinkedIn posts, the S&P 500 market generally leads the VIX market. Therefore, signals from the S&P 500 can also be used to trade VIX futures.

Let me know your thoughts in the comments below.