The weekend (or Monday) effect in the stock market refers to the phenomenon where stock returns exhibit different patterns on Mondays compared to the rest of the week. Historically, there has been a tendency for stock prices to be lower on Mondays. Various theories attempt to explain the weekend effect, including investor behaviour, news over the weekend, and the impact of events occurring during the weekend on market sentiment.
In this post, we’ll investigate the weekend effect in the market indices using data from Yahoo Finance spanning January 2001 to December 2023. Specifically we choose SPY, which tracks the SP500, and the volatility index, VIX.
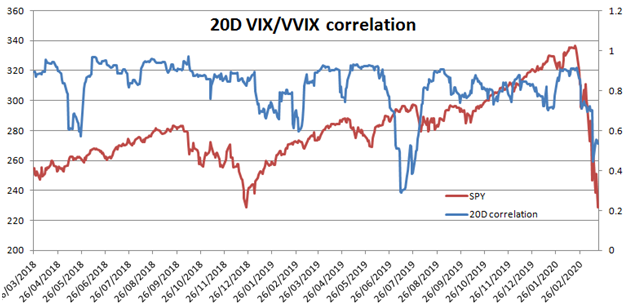
Our strategy involves taking a long position in SPY at Friday’s close and exiting the position at Monday’s close, or the next business day’s close if Monday is a holiday. The figure below depicts the cumulative, non-compounded return of the strategy.
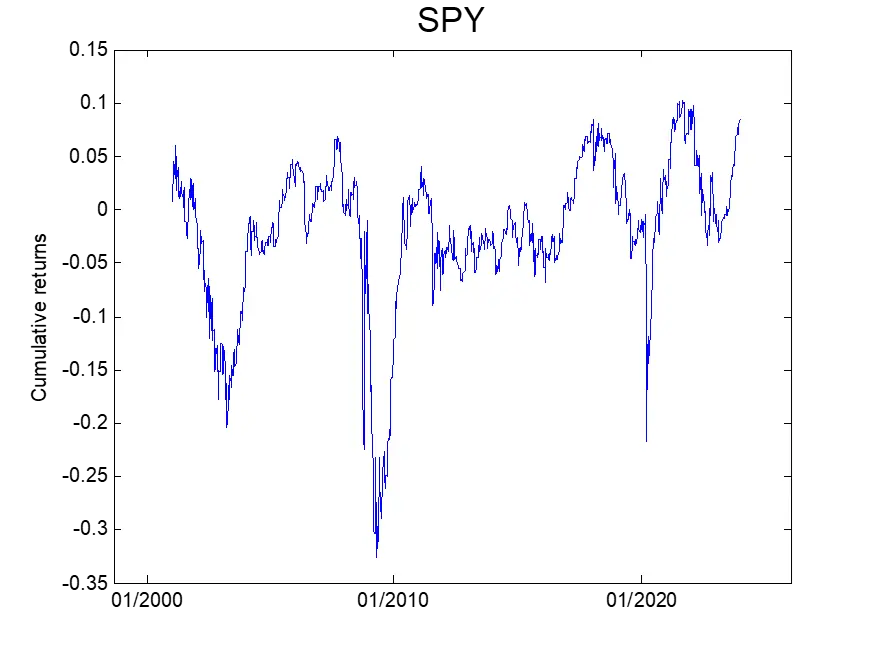
From the figure, we observe that holding SPY over the weekend resulted in negative returns during the GFC, Covid pandemic, and the recent 2022 bear market. The overall return is flat-ish, indicating a low reward/risk ratio for holding the SPY over the weekend.
Next, we analyze the change in the VIX index during the weekend. We compute the change in the VIX index from Friday’s close to the close of the next business day and plot the cumulative difference in the figure below. A noticeable upward trend is observed in the cumulative difference. This result indicates that maintaining a long vega/gamma position over the weekend would offer a favourable reward-to-risk trade.
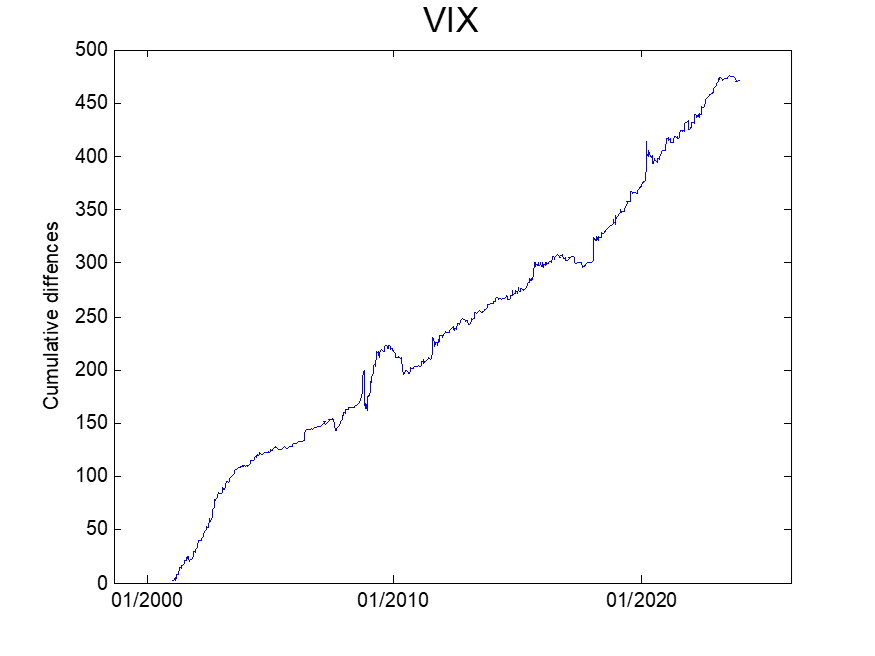
It’s important to note, however, that investing directly in the spot VIX is not possible. To confirm and capitalize on the weekend effect in the volatility index, one would have to:
- Trade a volatility ETN, or
- Trade a delta-hedged option position
Each of these approaches introduces additional risk factors, specifically 1- the roll yield and contango, and 2- PnL originating from gamma and theta. These issues will be addressed in the next installment.