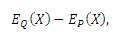A recent post on Bloomberg website entitled Rising VIX Paints Doubt on S&P 500 Rally pointed out an interesting observation:
While the S&P 500 Index rose to an all-time high for a second day, the advance was accompanied by a gain in an options-derived gauge of trader stress that usually moves in the opposite direction
The article refers to a well-known phenomenon that under normal market conditions, the VIX and SP500 indices are negatively correlated, i.e. they tend to move in the opposite direction. However, when the market is nervous or in a panic mode, the VIX/SP500 relationship can break down, and the indices start to move out of whack.
In this post we revisit the relationship between the SP500 and VIX indices and attempt to quantify their dislocation. Knowing the SP500/VIX relationship and the frequency of dislocation will help options traders to better hedge their portfolios and ES/VX futures arbitrageurs to spot opportunities.
We first investigate the correlation between the SP500 daily returns and change in the VIX index [1]. The graph below depicts the daily changes in VIX as a function of SP500 daily returns from 1990 to 2016.
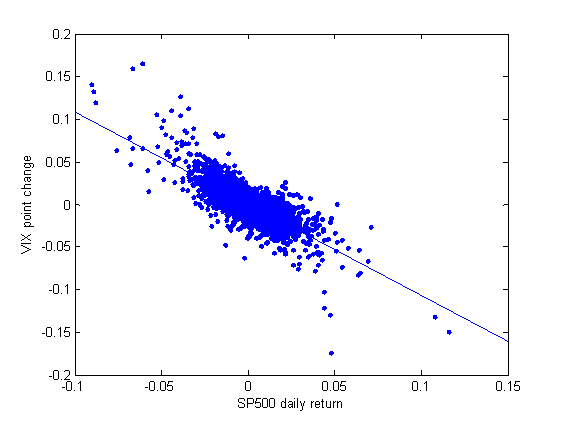
We observe that there is a high degree of correlation between the daily SP500 returns and daily changes in the VIX. We calculated the correlation and it is -0.79 [2].
We next attempt to quantify the SP500/VIX dislocation. To do so, we calculated the residuals. The graph below shows the residuals from January to December 2016.
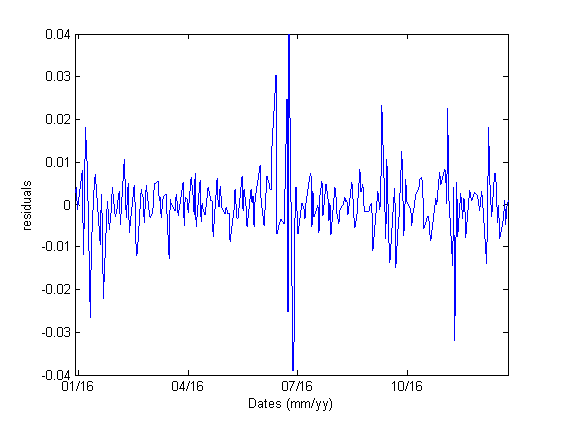
Under normal market conditions, the residuals are small, reflecting the fact that SPX and VIX are highly (and negatively) correlated, and they often move in lockstep. However, under a market stress or nervous condition, SPX and VIX can get out of line and the residuals become large.
We counted the percentage of occurrences where the absolute values of the residuals exceed 1% and 2% respectively. Table below summarizes the results
| Threshold | Percentage of Occurrences |
| 1% | 17.6% |
| 2% | 3.9% |
We observe that the absolute values of SP500/VIX residuals exceed 1% about 17.6% of the time. This means that a delta-neutral options portfolio will experience a daily PnL fluctuation in the order of magnitude of 1 vega about 17% of the time, i.e. about 14 times per year. The dislocation occurs not infrequently.
The Table also shows that divergence greater than 2% occurs less frequently, about 3.8% of the time. This year, 2% dislocation happened during the January selloff, Brexit and the US presidential election.
Most of the time this kind of divergence is unpredictable. It can lead to a marked-to-market loss which can force the trader out of his position and realize the loss. So the key in managing an options portfolio is to construct positions such that if a divergence occurs, then the loss is limited and within the allowable limit.
Footnotes:
[1] We note that under different contexts, the percentage change in VIX can be used in a correlation study. In this post, however, we choose to use the change in the VIX as measured by daily point difference. We do so because the change in VIX can be related directly to Vega PnL of an options portfolio.
[2] The scope of this post is not to study the predictability of the linear regression model, but to estimate the frequency of SP500/VIX divergence. Therefore, we applied linear regression to the whole data set from 1990 to 2016. For more accurate hedges, traders should use shorter time periods with frequent recalibration.