Would you rather choose a trading system that wins small amounts most of the time but when it loses, the loss is big? Or would you rather choose a trading system that loses small amounts most of the time but when it wins, the gain is big? In this blog post, we will examine such systems from the risk of ruin perspective.
The risk of ruin is the probability of an investor’s eventual bankruptcy due to a series of losses that exceed his/her capital. It is essential for any trader to understand their risk of ruin, as it will heavily influence the trading system they ultimately develop.
We will use Monte Carlo simulations to perform our analysis. We examine the following 3 trading systems
| System | Percent win |
Win |
Loss |
Expectancy |
|
A |
10% |
$90 |
$10 |
0 |
|
B |
50% |
$18 |
$18 |
0 |
|
C |
90% |
$10 |
$90 |
0 |
For each system, we generate 1000 trades randomly. If a trade is a win, then we’ll make the amount in the column “Win”, and if it’s a loss, then we’ll lose the amount in the column “Loss”. For example, for system A, if we win, we make $90 and if we lose, we lose $10.
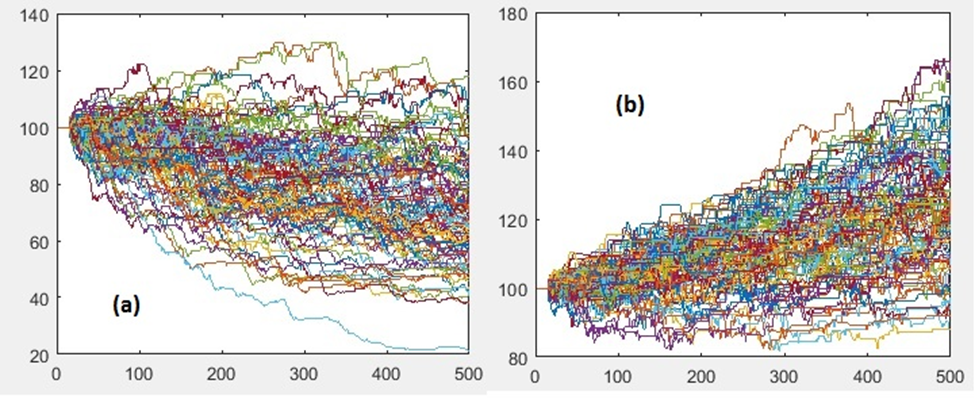
To simplify the analysis, we assume that all 3 systems have zero expectancies. The total winning/losing amounts of each system equal $9000. We start with an initial capital of $1000. The figure below shows the first 100 simulated paths for system A. It’s clear that the system has zero expectancy as the terminal wealth equals the starting capital.
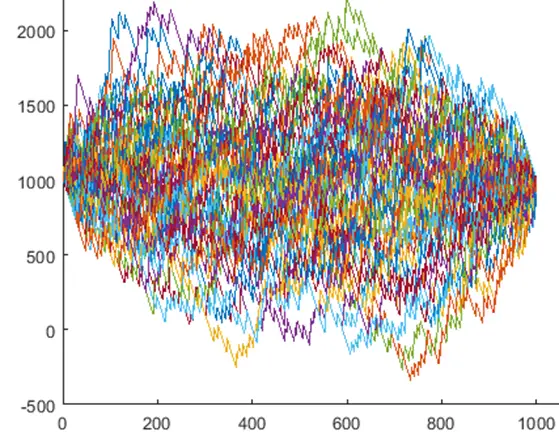
To calculate the probability of ruin, we first count the number of paths that go below $0 at any time in their evolutions. We then divide the number of such paths by the number of iterations which is 10000.
The table below summarizes the results.
|
System |
Risk of Ruin |
|
A |
10.22% |
|
B |
0.18% |
| C |
9.95% |
We can see from the results that system B has the lowest probability of ruin. This confirmed that traders should avoid systems that have high win percentages but suffer occasional large losses. Short volatility trading systems are in this category. Traders should also avoid systems that have low percentage win rates.